官方题解:Link
首先考虑暴力,具体来说可以从 SG 函数的角度思考。
如果一个位置可行那么设为 $1$,不可行则设为 $0$。
那么贝茜的操作即取 AND,FJ 的操作即取 OR。
见官方题解图:
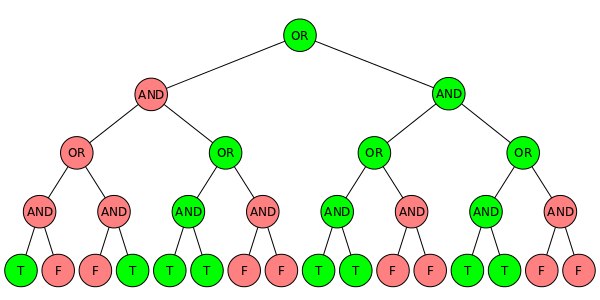
我们可以逐步确定取牌的策略,即先尝试取 B,检验是否可行,若不可行,取 T,(这样做是因为还有字典序最小的要求)。
暴力检验是 $O(2^{2n})$ 的。
接着我们发现 OR 和 AND 都有短路的性质,即 OR 中出现了一个 $1$ 之后就会停止运算,AND 类似。
我们可以随机的选择先计算哪一颗子树,再运用短路的性质剪枝。我们可以考虑证明这样做的时间复杂度。
设 $f(d)$ 为一颗深度为 $d$ 的子树结果为 $0$ 的计算次数,$t(d)$ 为结果为 $1$ 的计算次数。
注意到德·摩根定律:
$$
P \land Q = \lnot (\lnot P \lor \lnot Q)
$$
所以 AND 与 OR 本质相同,故不妨假设所有操作都在 OR 上。
对于 $f(d)$,根据德·摩根(注意取反)有:
$$
f(d) = 2 t(d-1)
$$
对于 $t(d)$,当我们只有一个 $1$ 子树的时候最劣:
$$
t(d) = f(d-1) + \frac{1}{2} t(d-1)
$$
故:
$$
t(d) = \frac{1}{2} t(d-1) + 2 t(d-2)
$$
所以:
$$
t(d) = (\frac{1+\sqrt{33}}{4})^d
$$
所以检验的时间复杂度是:$O((\frac{1+\sqrt{33}}{4})^{2n})$ 的。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| #include<bits/stdc++.h>
using namespace std;
const int maxn=15;
mt19937 rnd(time(0));
int n,m,K;
int a[maxn+5][10];
char s[maxn+5];
inline int Calc(int st,int x,int c,int t){
return ((a[st][(c<<2)|(t<<1)]+1ll)*x
+a[st][(c<<2)|(t<<1)|1])%m;
}
bool Check(int st,int x,int c){
int t=rnd()&1;
if(st>(n-1)<<1) return (x<=K)||(-x+m<=K);
if(st&1) return Check(st+1,x,t)||Check(st+1,x,!t);
else{
return Check(st+1,Calc(st>>1,x,c,t),t)
&&Check(st+1,Calc(st>>1,x,c,!t),!t);
}
}
signed main(){
scanf("%d%d%d",&n,&m,&K);
scanf("%s",s);
for(int i=0;i<n;i++)
for(int j=0;j<8;j++)
scanf("%d",&a[i][j]);
int x=0;
for(int i=0;i<n;i++){
if(Check(i<<1,x,1)){
putchar('B');
x=Calc(i,x,1,s[i]=='B');
}
else{
putchar('T');
x=Calc(i,x,0,s[i]=='B');
}
}
return 0;
}
|
