我们如何计算波峰和波谷的数量和呢？

sequence-1

如上图，我们发现波峰，波谷处于一段上升子段（长度大于等于 $2$）的开头与结尾处（需要特殊处理左右两边）。

故我们需要维护上升子段的数量，左、右两边是否为上升子段，三个信息。

于是我们考虑DP，从小到大依次插入 $1$ 至 $n$ 到序列中。

这样我们每次都将一个大于原序列中所有数的数插入进序列中，考虑其对原序列的影响。

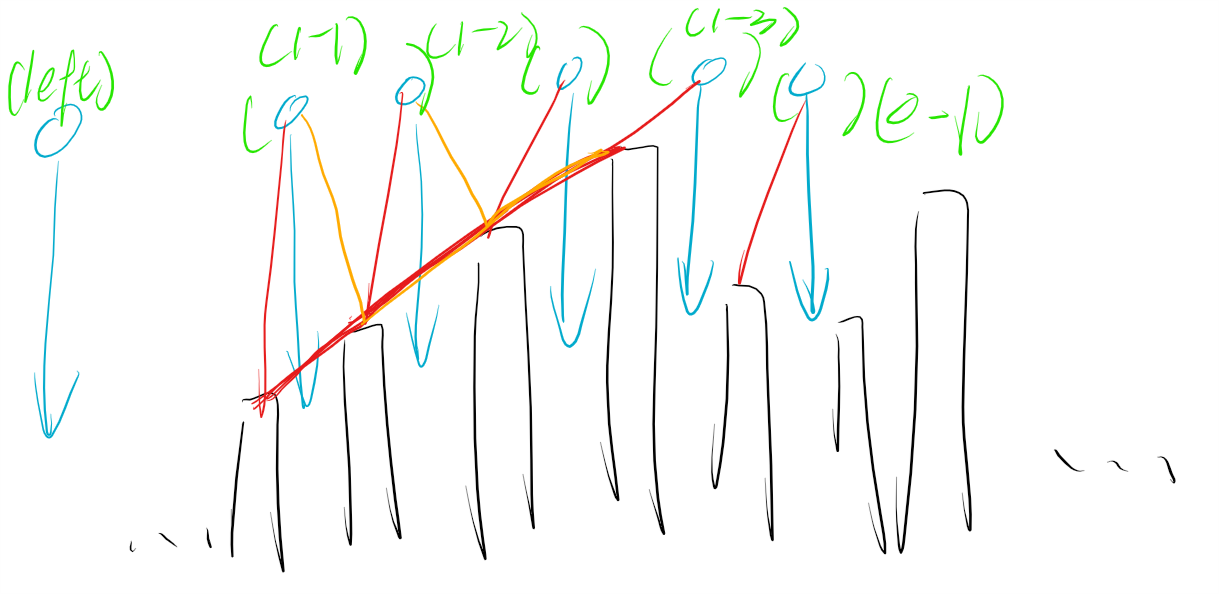
sequence-2

我们可以将插入位置其分成五类 left、1-1、1-2、1-3、0-1。

为了对每一类计数，我们还需要记录有多少个数在上升子段中。

我们设状态 $f(i,j,k,l,r)$ 表示考虑到 $i$，共有 $j$ 个上升子段，有 $k$ 个数处于上升子段中，左侧在、不在上升子段中（$l=1$ 表示在，$l=0$ 表示不在），右侧在、不在上升子段中（$r$ 同理），的排列的数量。

我们考虑这五类插入位置的数量，与对序列造成的改变。

同时考虑上对左右两边的特判。

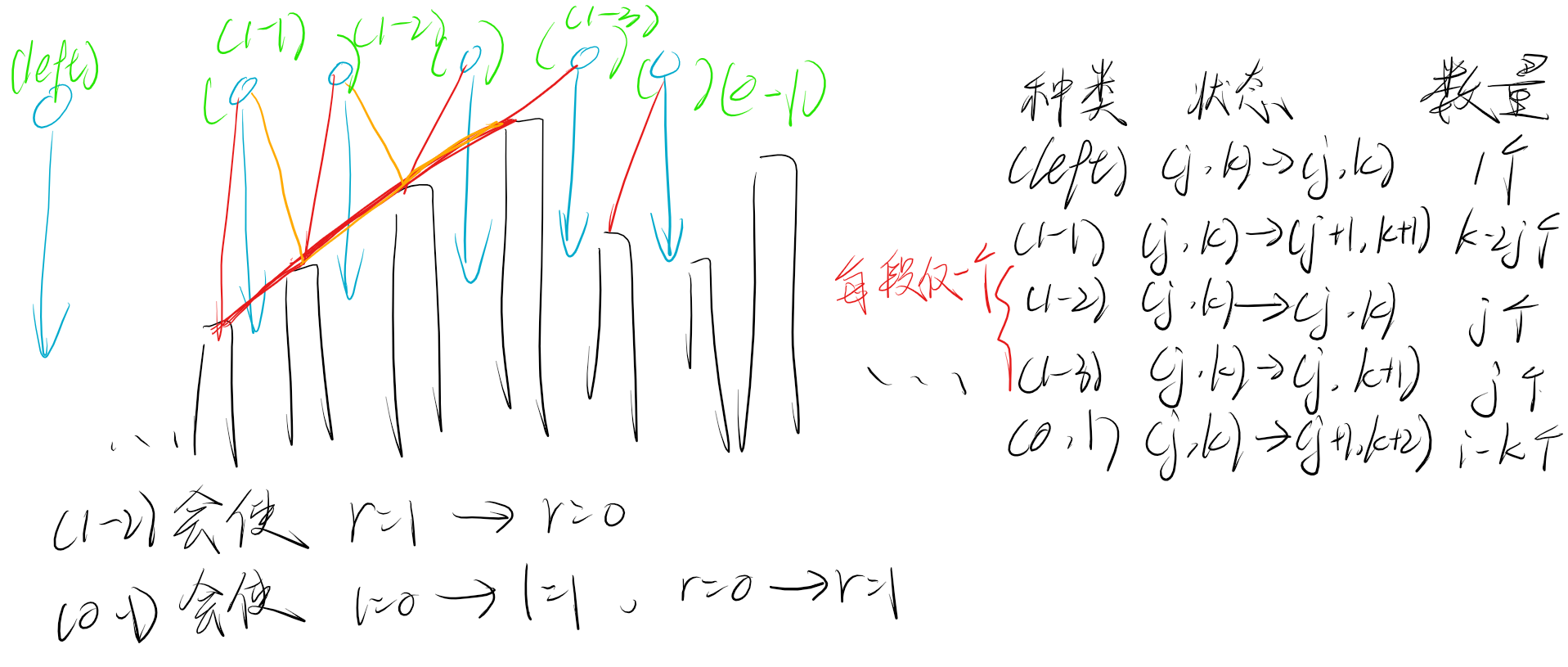
sequence-3

$f(i,j,k,l,r)$ 的波峰和波谷数量和为 $2j-l-r$。

实现上考虑刷表，从 $2$ 开始刷，注意特判 $n=1$ 和 $n=2$。

$f(2,0,0,0,0) = 1$

$f(2,1,2,1,1) = 1$

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
#include<bits/stdc++.h>
using namespace std;
#define int long long 
const int maxn=200;
const int mod=998244353;
int n,m;
int f[maxn+5][maxn+5][maxn+5][2][2];
int ans;
inline void Add(int &x,int y){x=(x+y)%mod;}
inline void Solve(){
    f[2][1][2][1][1]=1;
    f[2][0][0][0][0]=1;
    for(int i=2;i<n;i++){
        for(int j=0;j<=i;j++){
            for(int k=2*j;k<=i;k++){
                for(int l=0;l<=1;l++){
                    for(int r=0;r<=1;r++){
                        //1-2
                        if(r){
                            Add(f[i+1][j][k][l][0],f[i][j][k][l][r]);
                            Add(f[i+1][j][k][l][r],f[i][j][k][l][r]*(j-1));
                        }
                        else Add(f[i+1][j][k][l][r],f[i][j][k][l][r]*j);
                        //1-3
                        Add(f[i+1][j][k+1][l][r],f[i][j][k][l][r]*j);
                        //1-1
                        Add(f[i+1][j+1][k+1][l][r],f[i][j][k][l][r]*(k-2*j));
                        //0-1
                        if(l&&r)
                            Add(f[i+1][j+1][k+2][l][r],f[i][j][k][l][r]*(i-k));
                        else if(l){
                            Add(f[i+1][j+1][k+2][l][1],f[i][j][k][l][r]);
                            Add(f[i+1][j+1][k+2][l][r],f[i][j][k][l][r]*(i-k-1));
                        }
                        else if(r){
                            Add(f[i+1][j+1][k+2][1][r],f[i][j][k][l][r]);
                            Add(f[i+1][j+1][k+2][l][r],f[i][j][k][l][r]*(i-k-1));
                        }
                        else{
                            Add(f[i+1][j+1][k+2][l][1],f[i][j][k][l][r]);
                            Add(f[i+1][j+1][k+2][1][r],f[i][j][k][l][r]);
                            Add(f[i+1][j+1][k+2][l][r],f[i][j][k][l][r]*(i-k-2));
                        }
                        //left
                        Add(f[i+1][j][k][0][r],f[i][j][k][l][r]);
                    }
                }
            }
        }
    }
    for(int j=0;j<=n;j++)
        for(int k=2*j;k<=n;k++)
            for(int l=0;l<=1;l++)
                for(int r=0;r<=1;r++)
                    if(m==2*j-l-r)
                        Add(ans,f[n][j][k][l][r]);
    printf("%lld",ans);
}
signed main(){
    scanf("%lld%lld",&n,&m);
    if(n==1){
        if(m) puts("0");
        else puts("1");
    }
    else if(n==2){
        if(m) puts("0");
        else puts("2");
    }
    else Solve();
    return 0;
}